Recursion is a fundamental concept in computer science and programming that allows a function to call itself in order to solve a problem. This technique is often utilized in scenarios where a problem can be divided into smaller, more manageable subproblems, effectively transforming complex algorithms into simpler, more elegant solutions. While recursion can lead to code that is both concise and readable, it also requires careful consideration regarding its implementation, particularly with respect to performance, memory usage, and stack overflow issues. In this article, we will provide a detailed examination of recursion, exploring its principles, practical applications, and the balance between recursive and iterative approaches. Through this exploration, we will elucidate how recursion can serve as a powerful tool in a programmer’s arsenal while highlighting the key challenges and considerations that accompany its use.
Table of Contents
- Understanding the Fundamental Principles of Recursion
- Analyzing Common Recursion Patterns and Their Applications
- Performance Considerations and Optimization Techniques for Recursive Functions
- Best Practices for Implementing and Debugging Recursive Algorithms
- Key Takeaways
Understanding the Fundamental Principles of Recursion
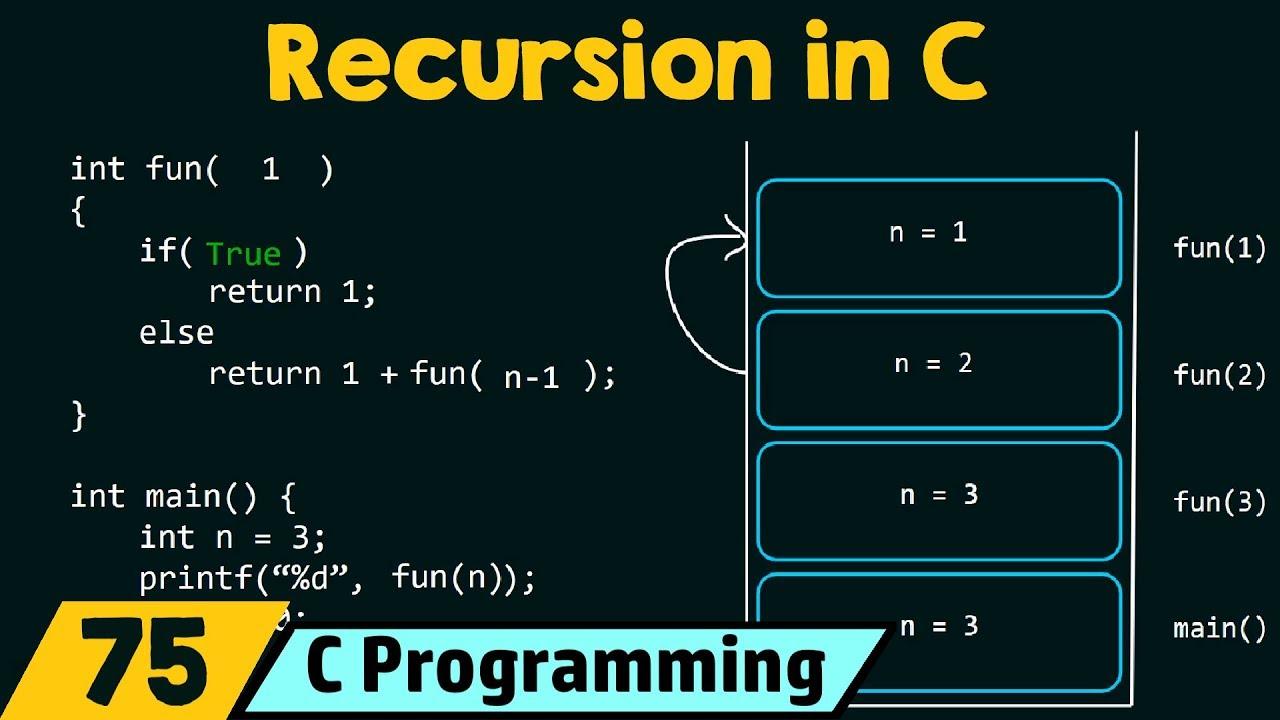
Recursion is a fundamental concept in programming that allows a function to call itself to solve a problem. This technique leverages the power of divide-and-conquer, breaking down complex problems into more manageable subproblems. A recursive function typically consists of two critical components: a base case and a recursive case. The base case acts as a termination point that prevents infinite recursion by providing a straightforward solution for the simplest instance of the problem. The recursive case, on the other hand, is where the function calls itself, tackling a smaller segment of the original problem. This interplay between the two cases is essential for the functionality and efficiency of recursive algorithms.
The benefits of recursion can be profound, especially when dealing with problems that involve hierarchical structures or repetitive patterns. Common applications include algorithms for traversing trees, searching, and sorting. However, it’s crucial to balance the depth of recursion with programming language constraints, as excessive recursion can lead to stack overflow errors. Below is a brief comparison of recursion and iteration, highlighting their respective characteristics:
| Aspect | Recursion | Iteration |
|---|---|---|
| Structure | Function calls itself | Loop constructs (for, while) |
| Memory Usage | Higher due to call stack | Lower, generally more efficient |
| Readability | Often clearer for complex problems | Can be less intuitive for nested structures |
Analyzing Common Recursion Patterns and Their Applications
Recursion in programming can be categorized into several common patterns, each with unique characteristics and use cases. Understanding these patterns enables developers to make informed choices when designing algorithms. Some widely recognized recursion patterns include:
- Base Case Identification: This pattern emphasizes the importance of defining a terminating condition for the recursive calls, ensuring that they stop at the right moment.
- Divide and Conquer: This technique involves breaking a problem into smaller subproblems, solving them independently and combining their results, as seen in algorithms like merge sort and quicksort.
- Dynamic Programming: Recursion is often paired with memoization to store previously calculated results, which reduces computation time in problems like the Fibonacci sequence or the knapsack problem.
Each of these patterns not only highlights the versatility of recursion but also showcases its practical applications in solving complex problems with simplicity and clarity. To further illustrate, consider the following table that summarizes some popular recursive algorithms along with their applications:
| Algorithm | Application |
|---|---|
| Factorial | Combinatorial problems and permutations |
| Fibonacci Series | Mathematical modeling and dynamic programming |
| Depth-First Search | Graph traversal and pathfinding |
| Tower of Hanoi | Teaching recursion principles |
Performance Considerations and Optimization Techniques for Recursive Functions
When utilizing recursive functions, performance can become a critical issue, particularly with problems that have overlapping subproblems, such as those found in dynamic programming. A fundamental performance consideration is the time complexity, which can escalate dramatically with naive implementations due to the repeated calculations of the same values. For instance, consider the naive Fibonacci calculation, which exhibits exponential time complexity. To remedy this, technique like memoization can be employed. Memoization stores previously computed results, allowing the function to return these cached values instead of recalculating them, significantly improving execution time.
Another optimization technique is to minimize the depth of recursion. Deep recursive calls may lead to stack overflow errors, especially in languages that do not optimize tail calls. Tail recursion allows the compiler to optimize the call stack, effectively converting the recursion into a loop. To illustrate these differences, refer to the table below showing the performance impact of different approaches to the Fibonacci sequence:
| Method | Time Complexity | Space Complexity |
|---|---|---|
| Naive Recursion | O(2n) | O(n) |
| Memoization | O(n) | O(n) |
| Dynamic Programming | O(n) | O(1) |
| Tail Recursion | O(n) | O(1) |
Best Practices for Implementing and Debugging Recursive Algorithms
When implementing recursive algorithms, certain best practices can enhance both the readability and performance of your code. First, ensure that you clearly define a base case that stops the recursion. This prevents infinite loops and stack overflow errors. Additionally, use tail recursion where possible, as it can optimize function calls and improve performance in languages that support tail call optimization. It’s crucial to maintain a clean and organized code structure by separating the logic into smaller, manageable functions; this not only aids in understanding but also simplifies debugging. Consider using a helper function that wraps the recursive logic, allowing you to manage state or pass additional parameters without complicating the main function.
Debugging recursive algorithms can be challenging, but several strategies can make this process easier. Start by introducing comprehensive logging at each recursive call to track the flow of execution and understand how parameters change with each step. Use tracebacks to visualize the recursion tree, providing clarity on how many times a function is called and which paths are taken. If you encounter issues, apply the divide and conquer strategy to isolate and test parts of your algorithm independently. leverage unit testing methodologies to create tests for your recursive functions that cover various scenarios, ensuring correctness and robustness. Below is a brief comparison of standard practices for recursion versus iteration:
| Aspect | Recursion | Iteration |
|---|---|---|
| Readability | High for problems with natural recursive structure | Medium often requires additional control structures |
| Performance | Can be slower due to function calls | Generally faster due to direct loops |
| Memory Usage | Higher stack memory due to calls | Lower as it uses fixed memory space |
| Debugging Difficulty | High due to multiple states | Low simpler flow |
Key Takeaways
recursion stands as a fundamental concept in programming that encapsulates both elegance and complexity. Its ability to solve problems through self-referential methods provides a powerful tool in a developer’s arsenal, enabling elegant solutions for tasks such as tree traversals, factorial computations, and complex algorithm implementations. However, the intricacies of recursion require careful consideration, particularly regarding stack depth limitations and potential performance implications.
Understanding when and how to apply recursive techniques is pivotal in writing efficient and maintainable code. As we have explored, recursion can lead to more readable solutions, yet it demands a thorough understanding of the underlying mechanics to avoid pitfalls such as excessive memory usage and infinite loops.
As programming paradigms continue to evolve, recursion remains a relevant subject, prompting developers to refine their approach and deepen their understanding of algorithm design. By embracing recursion with a critical mindset, programmers can enhance their problem-solving capabilities and contribute to the creation of more sophisticated and efficient software systems.